Controle PID de Potência em Corrente Alternada - Arduino e TRIAC - Parte V
No último post escrevi uma introdução sobre PID (controle Proporcional, Integral e Derivativo), onde descrevi a teoria envolvida e o "P", ou seja, o controle Proporcional.
Os posts que compõem essa série podem ser clicados abaixo:
Controle de Pot. em CA - PID, Arduino e TRIAC - Parte I
Controle de Pot. em CA - PID, Arduino e TRIAC - Parte II
Controle de Pot. em CA - PID, Arduino e TRIAC - Parte III
Controle de Pot. em CA - PID, Arduino e TRIAC - Parte IV
Neste post, vamos falar dos controles Integral e Derivativo.
O controle Derivativo procura fazer com que o nosso sistema atue mais rápido ou mais devagar segundo a taxa de resposta do PV. Ou seja, a resposta do sistema será inversamente proporcional à taxa de variação (derivada, aí o nome) do PV. Quanto mais devagar o PV estiver variando, maior será a correção calculada.
Por fim, o controle Integral procura levar em conta quanto tempo estivemos afastados do set point. Ele é importante para tentar evitar que o sistema fique oscilando em torno do set point, oscilação que é causada pelas componentes Integral e Derivativa.
Resumindo:
Controle Proporcional: calcula o MV levando em conta a distância entre o set point e o valor da variável PV em um determinado instante.
Controle Integral: calcula o MV levando em conta o tempo em que o sistema fica distante do set point (SP).
Controle Derivativo: calcula o MV levando em conta a taxa de variação (velocidade com que varia, ou derivada) do PV.
Definindo parâmetros
A chave do controle PID é a gente definir qual é a proporção relativa de cada componente em nosso sistema de controle. Essa proporção, ou peso, é dada pelas contantes Kp, Ki e Kd.
Agora, como escolher o valor de cada constante no nosso controle? Bom, cada caso é um caso. Eu acho (e é minha opinião mesmo) que a gente tem que considerar vários fatores, já que o que importa é a curva que a gente quer de controle. Vc então tem que responder perguntas como:
- É necessário que o controle responda o mais rápido possível a uma perturbação?
- Ou isso não é tão importante, mas sim o valor presente deve evitar ao máximo ultrapassar o set point? Quando VP ultrapassa SP tempos uma sobrecarga, que pode ser importante ou não.
- O set point muda ou é constante?
- Se ele se altera às vezes, qual a faixa de valores em que ele varia? Ele varia bruscamente ou suavemente?
Todas essas questões vão influenciar a escolha dos parâmetros, que no fim é o que determina a forma da curva.
Como são três parâmetros que atuam de forma "coordenada", quer dizer, o valor de um parâmetro influencia no comportamento das outras componentes, o ajuste pode ser difícil. Pode-se adotar três caminhos:
- Ajuste manual (no popular, tentativa e erro): vai-se testando diferentes valores e verificando o resultado até que o sistema funcione do jeito que queremos.
Ao usar essa técnica, devemos levar em conta a seguinte tabela. Ela mostra o reflexo que um aumento num determinado parâmetro provoca no sistema:
Ou seja, vamos "mexendo" nos parâmetros considerando o seu efeito conforme a tabela acima.
- Cálculo dos parâmetros: nesse caso, a gente usa alguma regra para calcular os valores dos parâmetros de maneira a obter o resultado desejado.
Vou descrever um dos métodos para se calcular Kp, Ki e Kd, o método de Ziegler-Nichols. Consta que é o mais utilizado.
Esse método é heurístico, ou seja, uma vez que vc o use, não há garantia matemática que a solução é a melhor possível (nesse caso, o método seria chamado determinístico). Contudo, é bastante eficaz na maioria dos casos.
O método Z-N consiste em:
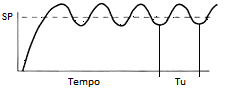
- Primeiro, zera-se Ki e Kd. Em seguida, varia, começando de zero, o valor de Kp até obter o valor de Ku, definido como o menor valor de Kp em que o sistema fica oscilando em torno do SP com uma velocidade constante. No gráfico abaixo vc vê o comportamento do circuito com Kp=Ku, Ki=0, Kd=0.
O período Tu da onda e o valor de Ku serão usados para calcular os outros parâmetros, conforme a tabela abaixo:
Se vc usar o Z-N para calcular seus parâmetros, tenha em mente que:
Os valores de Kp Ki e Kd calculados com o Z-N tendem a levar o comportamento do sistema para um ganho agressivo (o sistema se aproxima rapidamente do SP) e com isso, a tendência a sobrecarga. Se a sobrecarga for muito problemática, esse não é o método adequado para estimar os parâmetros, mas mesmo assim pode servir como ponto de partida.
- Mistura das técnicas acima: primeiro a gente calcula os parâmetros usando Z-N, mede o efeito. Em seguida, vamos tentando um ajuste fino "brincando" com as constantes para chegar ao resultado desejado.




Mauro, se eu entendi direito, ajustando corretamente os valores de Kp, Ki e Kd eu terei (teoricamente) uma constante no meu controle, ou seja, a minha leitura de feedback (sensor) terá uma variação de tensão próxima a 0, correto? MAAASSSS e se meu sistema se comportar bem com uma histerese razoavelmente alta? Nesse seu exemplo, vamos supor que meu sistema se comporte bem entre 55º a 65º? Eu consigo fazer isso sem fritar meu triac???
ResponderExcluirPor partes:
Excluir1) Ajustando corretamente os valores de Kp, Ki e Kd eu terei (teoricamente) uma constante no meu controle?
Não necessariamente. Disso depende o sistema que está sendo controlado. Se é um sistema de controle de temperatura, a troca de calor com o ambiente faz com que a MV seja maior que zero a maioria das vezes. Se for manter o nível de um tanque, a MV só será zero se o dreno do tanque estiver em zero.
Quanto às outras questões: como eu digo no texto, para escolher os k* vc tem que primeiro saber o que é problema para vc e o que não é. Se a histerese não é problema, um controle só proporcional daria. Mas existe alguma outra questão? Ex:
- Ocorrem variações de set point? Se ocorrem, quão rápido o sistema deve responder a elas?
- Quando o sistema é ligado (normalmente nesses casos a distância entre PV e SP é grande), é importante que ele atinja o set point rapidamente?
Ou seja, o ajuste de kp* não necessariamente garante uma saída próxima de zero, e a escolha depende dos seus objetivos.
Quanto a fritar o TRIAC, não sei se entendi: o que frita TRIAC é a corrente. Se ele estiver bem dimensionado, não é o fato dele estar sendo usado num controle PID que vai fritá-lo.
Este comentário foi removido pelo autor.
ResponderExcluirBoa tarde uma questão estou a fazer um projecto com o arduino em que tenho 3 sensores de corrente e tenho uma tensão fixa. Como se calcula a potencia e corrente hora e posteriormente como se calcula potencia e corrente dia???
ResponderExcluirO meu problema também é fazer a programação disto portanto se me puderem dar uma ajuda agradeço.
cumprimentos
Wilson,
ExcluirExistem 3 tipos de potência em corrente alternada. Se a sua carga for só resistiva (não tiver motor, por exemplo), a potência é o produto da tensão pela corrente.
Não sei se entendi bem a sua pergunta, se não, insista...
[],
Mauro